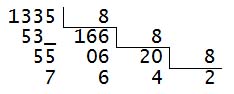Vimos anteriormente como converter a representação de um número inteiro positivo de uma base (b) para a base (10). Vamos ver agora como se faz a conversão inversa.

Considere-se o número seguinte em base (b):

Número em base (b):  a_na_n-1a_n-2…a₂a₁a₀

Este número pode ser representado da seguinte forma em base (10):

a_n x bⁿ + a_n-1 x b^n-1 + a_n-2x b^n-2…  + a₂ x b² + a₁ x b¹ + a₀ x b⁰

Se dividirmos este número e, depois, os cociente sucessivamente por b, obtêm-se os a_i do número original.

(a_nbⁿ + a_n-1b^n-1 + a_n-2 b^n-2… + a₂b² + a₁b¹ + a₀b⁰) / b

Resultado 1ª divisão:

Cociente: a_nb^n-1 + a_n-1b^n-2 + a_n-2 b^n-3… + a₂b¹ + a₁b⁰
Resto: a₀

Resultado 2ª divisão:
Cociente: a_nb^n-2 + a_n-1b^n-3 + a_n-2 b^n-4… + a₂b⁰
Resto: a₁

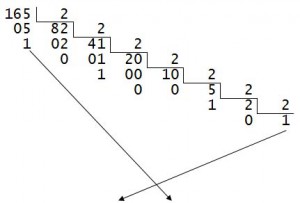
Exemplo: Converter para base 2 o número 165₍₁₀₎

Resultado:              10100101₍₂₎

Exercícios:

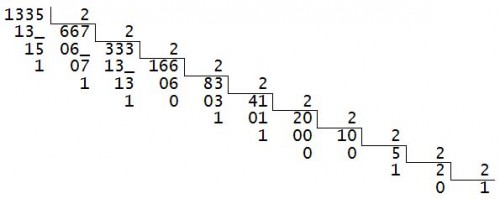
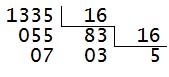
Converter o número 1335₍₁₀₎ para base 2, 8 e 16.

Em base 2: 10100110111₍₂₎

Em base 2: 2467₍₈₎

Em base 16: 537₍₁₆₎