Arquitetura de Computadores

Números fracionários – Converter base (10) para base (b)

Considere-se o número em base (b):  0,a_-1a_-2…a_-n(b)

O mesmo número pode ser representado em base 10 da seguinte forma:

a_-1 x b^-1 + a_-2 x b^-2 + …  + a_-n x b^-n₍₁₀₎

A conversão de um número fracionário de base (b) para (10) pode ser feita por multiplicação da parte fracionária dos produtos sucessivamente por b. Em cada multiplicação obtém-se, à esquerda da vírgula, um a_i do número pretendido na base (b).

(a_-1 x b^-1 + a_-2 x b^-2 + …  + a_-n x b^-n) x b

Resultado da 1ª multiplicação:

a_-1 x b⁰ + a_-2 x b^-1 + …  + a_-n x b^-n+1

O que corresponde ao número:

a_-1,a_-2…a_-n

Depois multiplica-se apenas a parte fracionária:

0,a_-2…a_-n

Ou seja:

(a_-2 x b^-1 + …  + a_-n x b^-n+1) x b

Resultado da 2ª multiplicação:

a_-2 x b⁰ + a_-3 x b^-1 + …  + a_-n x b^-n+2

O que corresponde ao número:

a_-2,a_-3…a_-n

Por fim constrói-se o número, com base nos a_i.

Resultado final:  0,a_-1a_-2…a_-n

Exemplo: Passar 0,5625₍₁₀₎ para base 2

0,5625 x 2 = 1,125   extrai-se um 1 (inteiro)
0,125 x 2 = 0,25     extrai-se um 0 (inteiro)
0,25 x 2 = 0,5       extrai-se um 0 (inteiro)
0,5 x 2 = 1,0        extrai-se um 1 (inteiro)

0,5625₍₁₀₎ = 0,1001₍₂₎

Exercício: Passar 12,3125₍₁₀₎ para base 2

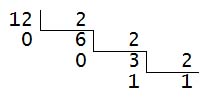
12₍₁₀₎ = 1100₍₂₎

0,3125 x 2 = 0,625
0,625 x 2 = 1,25
0,25 x 2 = 0,5
0,5 x 2 = 1,0

12,3125₍₁₀₎ = 1100,0101₍₂₎